NUMERICAL METHOD LAB 1 :Bisection Method:

Bisection method is used to find the real roots of a nonlinear equation. The process is based on the ‘Intermediate Value Theorem‘. According to the theorem “If a function f(x)=0 is continuous in an interval (a,b), such that f(a) and f(b) are of opposite nature or opposite signs, then there exists at least one or an odd number of roots between a and b.”

Features of Bisection Method:

Type – closed bracket
No. of initial guesses – 2
Convergence – linear
Rate of convergence – slow but steady
Accuracy – good
Programming effort – easy
Approach – middle point

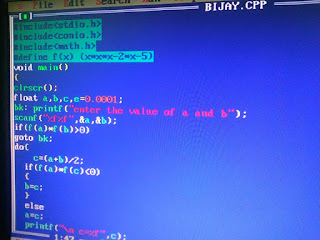
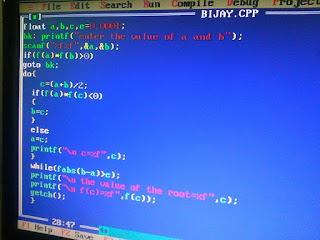
Bisection Method Algorithm:

Start
Read x1, x2, e
*Here x1 and x2 are initial guesses
e is the absolute error i.e. the desired degree of accuracy*
Compute: f1 = f(x1) and f2 = f(x2)
If (f1*f2) > 0, then display initial guesses are wrong and goto (11).
Otherwise continue.
x = (x1 + x2)/2
If ( [ (x1 – x2)/x ] < e ), then display x and goto (11).
* Here [ ] refers to the modulus sign. *
Else, f = f(x)
If ((f*f1) > 0), then x1 = x and f1 = f.
Else, x2 = x and f2 = f.
Goto (5).
*Now the loop continues with new values.*
Stop